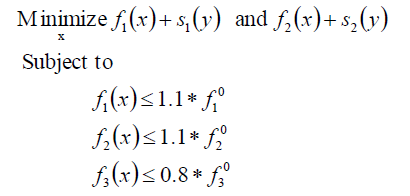{{ post.title }} 글 편집 글 편집 (이전 에디터) 作者 {{ post.author.name }} 完成日期

考虑麦克弗森悬架装置中缓冲器平顺偏差的刚架优化设计

<项目>

• 考虑麦克弗森悬架装置中缓冲器平顺偏差的刚架优化设计

<所使用的产品&功能>

• RecurDyn/Professional – Creating Body, Joint, Force Entities

• RecurDyn/AutoDesign – Performance Index, Design variable, Design Optimization, Robust Design Optimization, Design variable

<效果>

• 运用RecurDyn和AutoDesign提出了考虑制作公差的设计方法论

==========================================================================

本研究进行考虑减震器不平滑的不确定性对悬架装置机构性能的变化的刚体优化设计。设计变量是组成系统接头的坐标，概率常数是布减震器的刚度。然而，由于设计中考虑的性能指数是参数（车轮移动量）的Max/Min的函数，所以设计灵敏度求解非常困难。鉴于此，波恩研究中引入Meta模型方法，为了生成性能指数的近似函数，减少可靠性仿真所需要的仿真次数，通过近似函数计算了性能指数的样本方差。并将它们与顺序近似优化方法相结合，进行了悬架系统的刚健优化设计。并利用样本方差来验证优化设计的结果。

Case Study

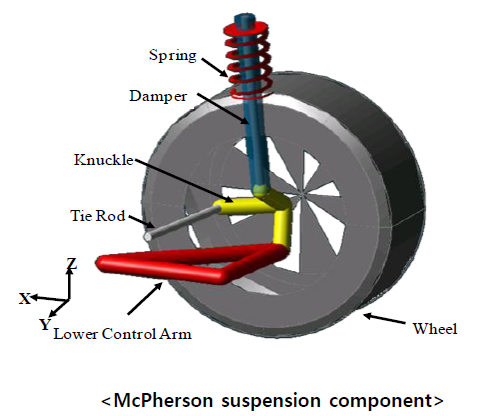
1) 悬挂装置型号
根据机构学连接形式，弹簧种类，左右轮是否独立等因素，悬架装置可分为多种形式。本研究选取了对机构学性能敏感的麦克弗森式作为设计对象。下图为麦克弗森式悬架系统的动力学模型，其主要组成部件为:Strut,Tie Rod，Knuckle，Lower Control Arm 各部件之间的连接由机构连接（Spherical，Revolute，Universal）和减震器元素（Spring，Damper，Bush）组成。悬架设备建模是用常用程序RecurDyn实现的。 以及本研究的设计目的是确定接头的位置。

2) 刚架优化设计问题的描述
提出了提高悬架设备性能的刚架优化设计问题并给出如下定义。目标函数试图最小化凸轮角的偏差（f1）和托偶角的偏差（f2）。考虑到它们的设计鲁棒性，此外，我们试图同时最小化它们在概率常数的不确定性下的样本偏差。此时，样本偏差利用Meta模型进行计算。由于悬架系统的主模型被认为设计的具备足够的鲁棒性，所以凸轮角和托梁角的上限偏差与主模型相比设置为10（%）余量作为约束条件. 建立了轮中心前后方向变化量与基本模型结果相比减为-20（%）的约束条件。 数学表述如下:

3) 鲁棒性优化设计结果
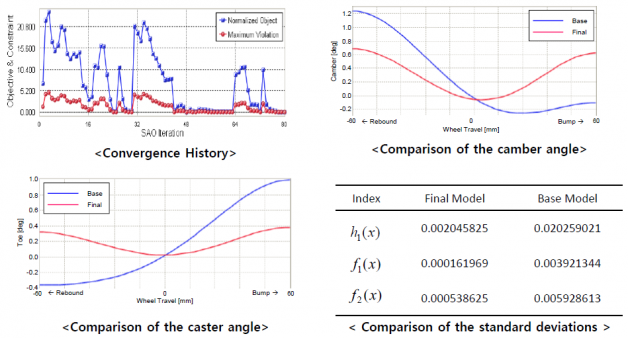
图显示了持续优化设计的收敛过程，每个迭代阶段都增加了一次新的仿真解。在SAO 1~48次过程中，不满足约束条件而有所振动的原因是Meta模型表达不准确的地方求“最优解”的现象。换句话说，在创建Meta模型时，由于初始实验点不足而导致的Meta模型提高精确度的过程。然后，SAO 64~75次过程被描述为在满足约束条件的“最优解”的附近，在目标函数中包含的近似样本方差误差的改进过程。

考察了性能指数Caster angle和Camber angle的结果，确认了得出了符合目标函数的结果。最终，通过标准偏差对表中优化设计值的鲁棒性性进行了探讨，结果比标准模型改善了90%以上 。

* 本内容是对2009年RecurDyn User’s Conference发布资料的重组。