{{ post.title }}
글 편집
글 편집 (이전 에디터)
{{ post.author.name }}
完成日期
| Version | {{ post.target_version }} | Product |
{{ product.name }}
|
|---|---|---|---|
| Tutorial/Manual | {{ post.manual_title }} | Attached File | {{ post.file.upload_filename }} |
紧紧的抓住钢尺的两端,它就会弯曲,但是如果继续弯曲的话,尺子最终就会折断。那么设计者在开始设计的时候就必须决定这个尺子是容易弯曲或者很难弯曲

图1. 弯曲的尺子
另一个例子是大桥,几辆重型卡车分别开上桥后,站在桥边的人会担心这座桥会被压塌。桥梁虽然没有塌陷,但是卡车在桥上行驶的时候大桥仍然会摇晃的厉害,开车的司机也很紧张。我们是否可以在卡车全部安全通过后说这座大桥的设计是安全的?答案是否定的。和前面的例子相同,设计师应该在设计初期对于卡车通过大桥时大桥能承受多重的重量以及大桥的变形程度等等予以确定。对于卡车经过大桥的例子来讲,虽然卡车经过大桥之后,大桥并没有倒塌,但是如果大桥自身摇晃的幅度过大的话,我们也很难说这个大桥是一个好的设计成果。

图2. 正在通过大桥的卡车
在这里大桥是否倒塌是强度的问题,而能弯曲的度则是刚度的问题。强度与刚度虽然各自的基准不同,但是都需要满足设计标准。
1. 仿真分析与柔性体
针对产品设计而言,即使不直接制作出现实产品进行试验,也可以利用计算机进行仿真分析得到对应产品的强度与刚度。 早期的设计曾经是在纸上用尺子和铅笔直接画出图面,之后随着计算机技术的飞速进步,工程师们开始在计算机上制作平面图纸,之后发展为在电脑上直接做出立体模型。这样使用计算式进行设计的方式称作计算机辅助设计(CAD: Computer Aided Design)。
仿真分析是使用已经在CAD软件中建好的模型进行的,但是CAD中建立的模型仅仅是用来表现外表和质量,无法计算其弯曲的程度。所以我们必须在仿真分析中进行额外的操作,使之弯曲。使之可以表现弯曲的方法是把外表的形状进行剪切,之后使用弹簧力将两块切片连接起来。每一块切片都叫做“单元 (Element)”。把所有切片连接在一起之后看起来很像一张网,把它们切成小块就叫做“网格 (Mesh)”。然后我们把它们弯曲时的形状叫做柔性体。
将切片拼凑起来表示曲折的形状的时候,之前生成的切片的尺寸越小,就越能精确的表现曲面。如果把它切得非常小的话,曲面也会变的非常平顺整齐。但是在现实中,我们无法将切片的格式增加到无穷大,所以工程师一般可以做出恰当的选择。与此同时,因为计算方法是使用某一数字(N)来代替这一无穷大的个数,所以我们称这个方法叫做“有限元法(Finite element method - FEM)”
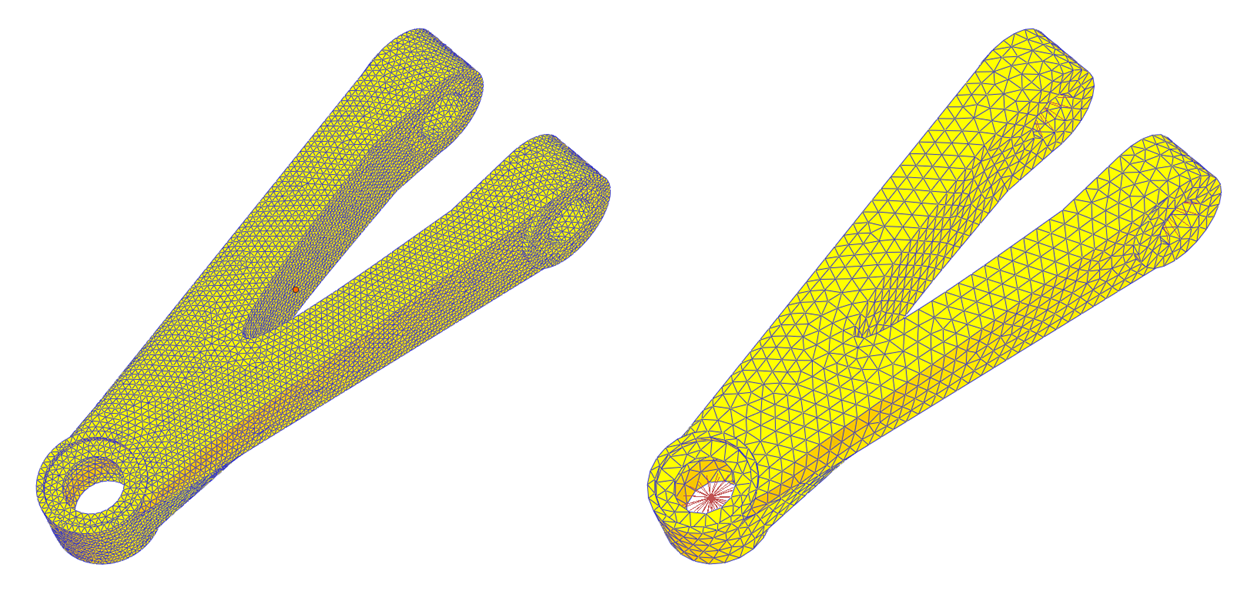
图3. 网格大小不同的柔性体
2. 振动
Lewis Carroll Epstein的著作『Thinking physics』中对振动做了如下的描述:
“在空间里荡漾的是波,随着时间波动的是振动。波不是固定在一个位置,而是从一个位置延伸到另一个位置。振动不是只发生在某一个瞬间,而是随着时间的推移发生的。除了根据时间和空间展开的特点外,波动和振动也有特殊之处。虽然在一块岩石上不能再叠加另一块岩石,但是波动和振动是可以同时出现在一个位置的。就像许多人同时在一个房间里唱歌一样。这样的歌曲和演奏交响乐的交响乐团所制造的振动叠加在一起产生的整个振动可以在唱片上记录下来。但是论个人惊讶的是,我们的耳朵可以通过聆听各种声源组成的犊砸的协奏曲获得不同的振动。然而我们非常享受这种振动”

图4. 交响乐团演奏现场
这篇文章把波动和振动分别用空间和时间进行了有趣的说明,在此,值得关注的内容有两点:
- 振动可以同时存在于同一个位置。(可叠加)
- 我们的耳朵在节奏曲中可以感受到每一个振动。(每个乐器音色的不同均可分辨)
这么说的原因是振动可以被分为各个单独的振动。例如<图5>是测量音叉的振动波形,可以将其分为多个单独的振动。
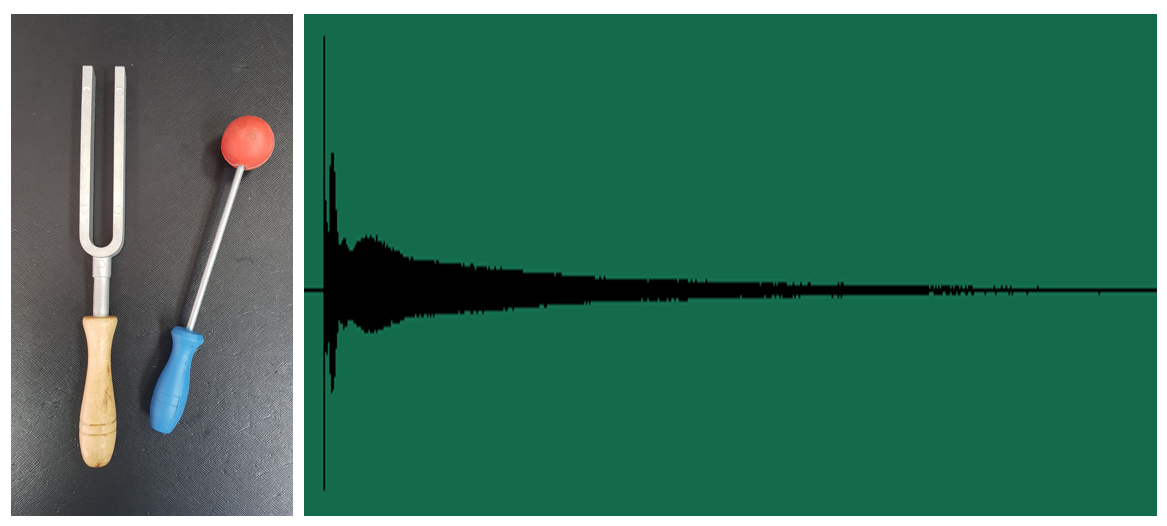
图5. 音叉的声波
将声波的振动进行快速傅里叶变换(Fast Fourier Transform)切换到不同频率的振动。 <图6>显示的是测量过的声波的傅里叶变换的结果,可以把整个振动分为366Hz和710Hz的简单振动。把整个振动分成各个频率的振动,这意味着把各个频率的振动加载一起就等于整个振动。
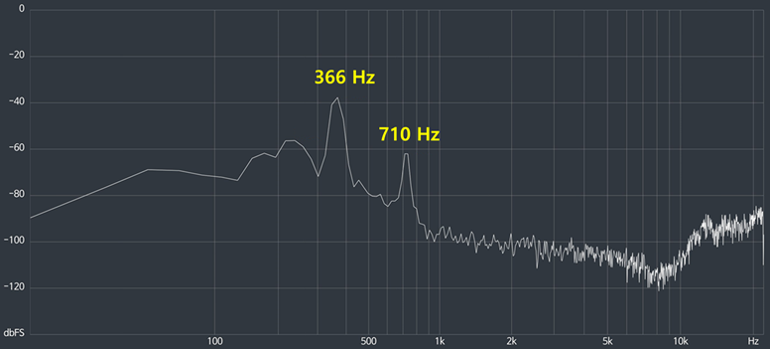
图6. 音叉振动的傅里叶变换结果(第一篇文章中提及的)
法国物理学教授傅里叶就这个问题做了比较通俗的说明,他说:“异常复杂的波实际上是几个简单的波的叠加。”这句话的意思是说,再复杂的波也可以分为几个简单波,只要将简单波叠加可形成相同的复杂波。<图7>显示的是复杂波(C)可以分为单纯波(A)和波(B)。
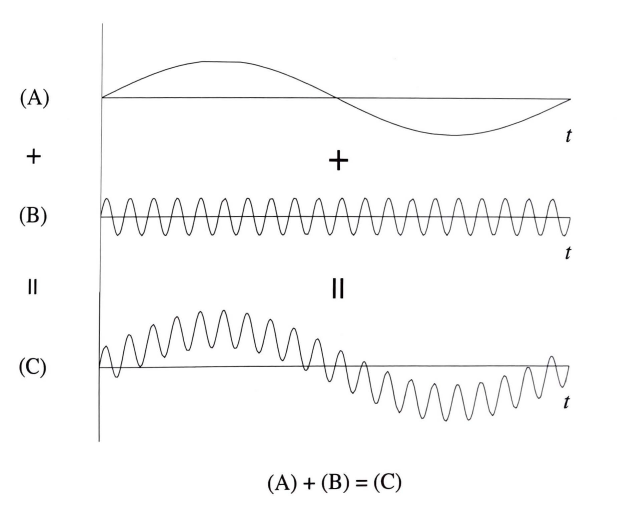
图7. 波的合成 (图片来源:《用数学学习的波动法则》- Transnational College of LEX)
即任何复杂的振动都可以拆分为多个简单振动,反之多个简单振动的叠加也会表现出其他复杂的振动。
后篇继续 (柔性体仿真与降阶模型(2/2)- 仿真,柔性体和振动
作者: FunctionBay总部 中国事业本部长 车泰辂



