{{ post.title }}
글 편집
글 편집 (이전 에디터)
{{ post.author.name }}
完成日期
| Version | {{ post.target_version }} | Product |
{{ product.name }}
|
|---|---|---|---|
| Tutorial/Manual | {{ post.manual_title }} | Attached File | {{ post.file.upload_filename }} |
在多体动力学仿真中,接触仿真是非常重要的。
几乎没有不包含接触的机械系统。另一方面,在CAE中,接触算法占据了计算量的大部分,对仿真时间和结果的精确度有很大的影响。因此,了解和使用接触原理和接触参数是至关重要的。
在CAE中使用的接触算法大多是PenaltyMethod,RecurDyn也是基于该方法进行接触计算的。 (即使是相同的 Penalty Method ,详细的算法也完全不同,因此不同软件的接触性能差别很大。)
该Penalty Method的特点是它使用“penetration”来计算接触。
许多RecurDyn初学者不知道这一部分就在使用接触,只要理解与之相关的简单内容,对以后定义接触,设置参数将大有帮助。
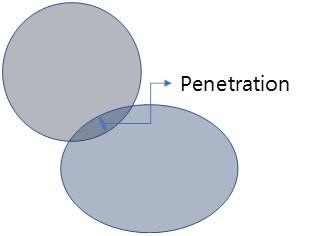
让我们看看两个实体的互相接触。

实际上,两个实体不会重合,但PenaltyMethod假设两个实体可以重合,并利用它们来计算接触力。
也就是说,两个实体可以重合,如下所示。 这时,两个实体之间的重叠量被称为penetration,或penetration depth。(penetration是渗透量的意思)
从现在开始的说明很重要。
(这里所讲的内容是为了便于理解,所以对于Penalty Method的正确理论内容,请查阅其他的论文等)。
Penetration
在Penalty Method中,当两个实体重合时,就像两个实体之间有一个弹簧,并计算接触力,认为弹簧已经压缩到penetration那么大。
也就是说,当Penetration的量称为δ时,接触力f = kδ计算。
(此时,k是接触参数之一的Stiffness Coefficient)

当然,正确的接触计算式如下,但从概念上理解为 f = kδ则更容易。
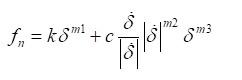
(省略对上述每个变量的说明)
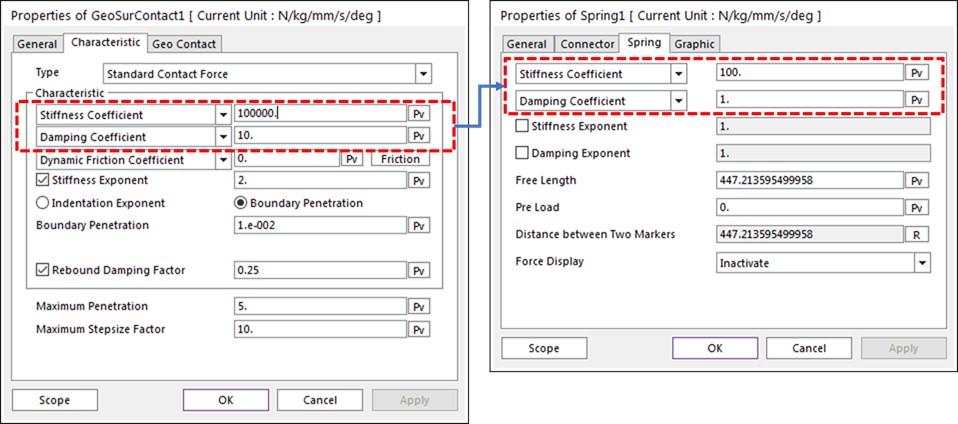
因此,Contact参数中的Stiffness/Damping Coefficient在概念上与弹簧的Stiffness/Damping Coefficient相同即可。
比如说,
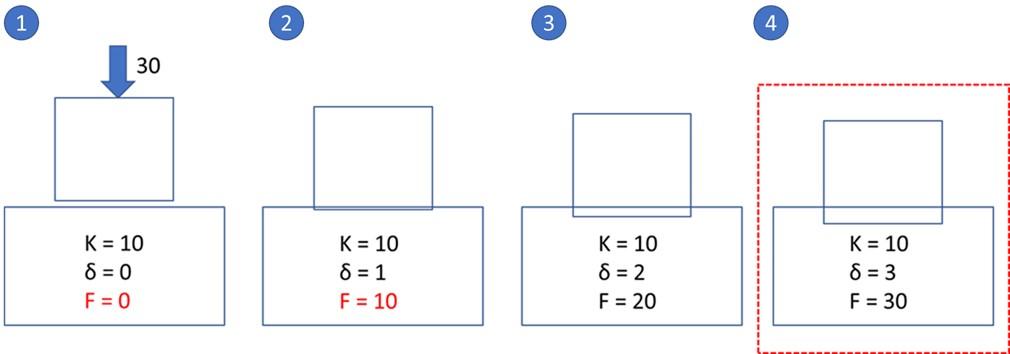
在以下情况下,penetration将增加,直到通过外力和 f=kδ计算的接触力达到平衡。(为方便起见,单位略去)。
在第1例中 ,由于上述箱体的重量,30的力是向下施加的,但由于, δ=0,所以不会发生接触力。箱体就会往下掉。
在第2种情况下 ,δ=1,虽然发生接触力,但由于是30>10,所以箱体仍然会下降。
在第3种情况下, 也是30>20,所以箱体下降。
在第4种情况下 ,达到30=30,从而达到力的平衡。(这里为了便于仿真,δ比较大,但实际上应该很小。)
因为f = kδ,所以如果将K(stiffness coefficient)设置得太小,那么只有当错误非常大时,才能达到平衡。但是,penetration是一个实际上不应该存在的值,所以它应该足够小才合理。 因此,K需要使用足够大的值。或者是RecurDyn的Geo Surface Contact,在Solid Contact中,K的默认值为100,000 N/mm)。
实际上,当下面是一个1千克重的箱体放在一个大箱体上时,接触力被计算为10N(按10m/s^2计算重力加速度),这时可以确定penetration=0.0001。(K=100000)

但是如果K太大,f = kδ 所以只要penetration稍微发生变化,产生的力的大小就会急剧变化。 这种力的急剧变化会对求解器仿真的稳定性造成不良影响。因此,使用合适的K来适应您需要的问题的情况是非常重要的。(过小会导致penetration大,准确度如果它太大,会影响求解器的仿真稳定性)
因此,需要在适当的范围内调节K。
(参考,在培养或减少K时,通常调节10倍,100倍,或0.1倍,0.01倍)。
本文从RecurDyn接触元素(Contact)初级教程第五弹-接触算法的基本原理-应用篇入手。
想对接触了解得更详细,请再参考下面的技巧。



